2012年一級注冊結構工程師考試普通物理考前沖刺（四）
發布時間：2012-07-25 共1頁
考前沖刺（四）
| 一、單選題 |
| 1．關于駐波，下列說法正確的是( )。 |
| 正確答案:A 解題思路：【解析】設沿正、負方向傳播的波分別為 y .gif) =Acos2π(t/T-x/λ)，y.gif) =Acos2π(t/T+x/λ)其合成波為 y=y +y=(2Acos2π(x/λ))cos2π(t/T)由上式可看出，合成后的點在做同周期的簡諧振動。但其各點的振幅｜2Acos2π(x/λ)｜與位置有關。在駐波中，同一分段上的各點有相同的振動相位，而相鄰兩分段上的各點，振動相位則相反，因此駐波行進過程中，沒有波形的定向傳播。 【點評】本題考查了駐波的基本性質。波節處，y=0，即波節是靜止的。各點的振幅｜2Acos2π(x/λ)｜與位置有關。駐波行進過程中，沒有波形的定向傳播。要清楚合成波方程中各物理量含義，在此題中，A表示振幅，A表示波長，y表示在t時刻的波動方程。 |
|
|
| 2．一束具有兩種波長的平行光垂直入射在光柵上，λ=600nm，λ=400nm，發現距中央明紋5cm處λ光的第k級主極大和λ光的第k+1級主極大相重合，放置在光柵與屏之間的透鏡的焦距f=50cm，試問上述k值為多少( )。 |
| 正確答案:C 解題思路：【解析】由題意λ光的第k級主極大和λ光的第k+1級主極大相重合，由夫瑯和費單縫衍射極小公式：asinφ=kλ 得：dsinφ =kλ，dsinφ=(k+1)λ；聯立求解得kλ=(k+1)λ；解得：k=λ/λ-λ=2。【點評】λ 光的第k級主極大和λ光的第k+1級主極大相重合是指λ光和λ光的衍射角相等。代入夫瑯和費單縫衍射極小公式：asinφ=kλ，聯立求解即得問題答案。 |
|
|
| 3．雙縫實驗中兩縫間距為0．15mm，屏幕到雙縫之間的距離為1．0m，測得屏幕上第一級和第十級暗紋之間的距離為36mm，則所用單色光的波長為( )。 |
| 正確答案:A 解題思路：【解析】由雙縫干涉暗紋公式： x 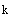 =±(2k+1)(Dλ/2d)k=0，1，2…得，第十級暗紋位置 x 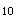 =21(Dλ/2d)第一級暗紋位置 x =3(Dλ/2d)所以，第十級和第一級暗紋之間的距離為 x 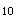-x9=9(Dλ/d)將已知數據d=0．15mm，D=1．0m=1000mm，x 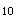-x=36mm代入上式解得，λ=0．60×10  mm=0．60μm【點評】考查暗紋中心距中央明紋中心的距離公式：x=±(2k+1)Dλ/2d，其中d為雙縫間距，λ為入射波的波長，D為屏幕到雙縫之間的距離。 |
|
|
| 4．在邁克爾孫干涉儀的一條光路放入一厚度為d，折射率為n的透明薄片，則這條光路的光程改變了( )。 |
| 正確答案:A 解題思路：【解析】由于邁克爾孫干涉儀中光線要穿過透明薄片2次，所以在邁克爾孫干涉儀的一條光路放入一厚度為d，折射率為n的透明薄片，則這條光路的光程改變了2nd-2d=2(n-1)d 【點評】本題主要考察邁克爾孫干涉儀光程的概念及光程改變量的計算，解題時要了解麥克爾孫干涉儀的基本原理。 |
|
|
5．己知t=0．5s的波形如圖所示，波速大小u=10m／s，若此時P點處媒質元的振動動能在逐漸增大，則波動方程為( )。 |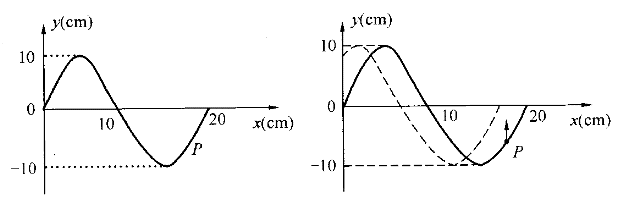
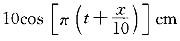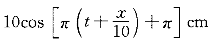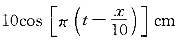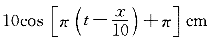正確答案:B 解題思路：【解析】由t=0．5s的波形曲線圖(a)知：A=10cm，λ=20cm，ω=2πν=2π(u/λ)=2π(10/20)=π·s 。且此時P點質元的動能在增大，應向平衡位置靠近，下一時刻的波形曲線如圖(b)中虛線所示。由此得出此波沿X負方向傳播，進而得出當t=0．5s時坐標原點(x=0)的質元在平衡位置且向y軸的反向運動。 即： ωt+φ=3π/2 故： φ=3(π/2)-ωt=3(π/2)-π/2=π 波動方程為 y=10cos[π(t+x/10)+π] 所以選B。 【點評】根據波形圖可以確定波長(λ)，振幅(A)。根據某點P振動圖可以確定周期(T)代入波速u=λ/T和角頻率ω=2π/T，求出波速和角頻率。根據P點質元的動能在增大，判斷P點應向平衡位置靠近，判斷出下一時刻的波形曲線如圖(b)中虛線所示。再根據波形圖的移動方向可以判斷波的傳播方向，得出此波沿x負方向傳播。根據初始條件t=0時，初位移y=y .gif) ，初速度υ=υ求解初相φ。運用選定系數法，設波動方程為y=Acos[ω(t-x/u)+φ]，分別將求得振幅(A)、波速(u)、角頻率ω、初相φ代入方程即可求解。 |
