2012年一級注冊結構工程師考試理論力學考前沖刺(八)
發布時間:2012-07-25 共1頁
考前沖刺(八)
| 一、單選題 |
1.質量為M的小車置于光滑水平面上,長為L的無重剛桿AB的B端固結一質量為m的小球,若剛桿在圖示位置無初速度地繞A軸向下轉動,當φ=0時小車的位移△x為( )。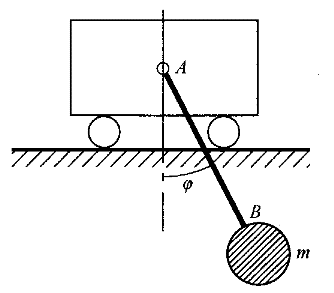 |
正確答案:B 解題思路:【解析】系統在水平方向所受合外力為零,由質心運動定理,系統質心在水平方向位置保持不變,以初始時刻A點位置作為坐標原點,則在運動始、末,系統質心在水平方向的坐標可分別表示為:x =mLsinφ/m+M,x =mLsinφ/m+M,x =M△x+m△x/m+M,由x =M△x+m△x/m+M,由x.gif) =x =x.gif) ,可得B正確。 ,可得B正確。【點評】本題主要考察對質心運動定理的理解、應用,以及物體系統質心的計算公式。 |
|
|
2.物塊重力為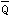 ,置于粗糙水平面上,接觸面處摩擦系數為f,拉力 ,置于粗糙水平面上,接觸面處摩擦系數為f,拉力 與水平線夾角為α,已知Q≥Fsinα,不致使物塊滑動的拉力 與水平線夾角為α,已知Q≥Fsinα,不致使物塊滑動的拉力 的大小應該是( )。 的大小應該是( )。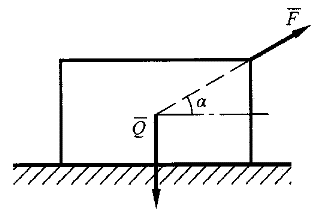 |
正確答案:A 解題思路:【解析】物塊與水平面的接觸壓力F =Q-F·sinα,最大靜摩擦力為F =Q-F·sinα,最大靜摩擦力為F =f·F =f·F 物塊不滑動,則必須F 物塊不滑動,則必須F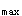 >F·cosα。 >F·cosα。【點評】本題主要考察有摩擦力作用時,物體的平衡問題。 |
|
|
| 3.點M沿半徑為R的圓周運動,其速度v=kt,k為常數,則點M的全加速度大小為( )。 |
正確答案:C 解題思路:【解析】點M的切向加速度a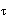 =dv/dt=k,法向加速度a =dv/dt=k,法向加速度a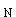 =(kt) =(kt) /R,全加速度大小為α= /R,全加速度大小為α=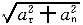 。 。【點評】本題主要考察點的圓周運動中加速度大小的計算。 |
|
|
4.圖示彈簧一端固定在O點,另一端A沿著半徑為R的圓弧滑動,若彈簧的原長為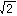 R,剛度系數為k,則在彈簧端點由A點到B點、B點到D點的過程中,彈性力所作的功W R,剛度系數為k,則在彈簧端點由A點到B點、B點到D點的過程中,彈性力所作的功W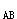 、W 、W 分別為( )。 分別為( )。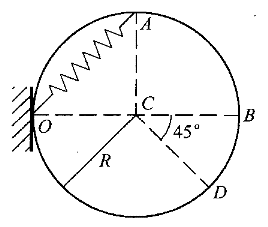 |
正確答案:D 解題思路:【解析】根據彈性力作功的公式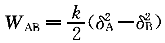 , ,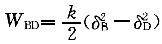 ,其中δ ,其中δ 、δ 、δ 、δ 、δ 分別為彈簧在A、B、D處的伸長量。 分別為彈簧在A、B、D處的伸長量。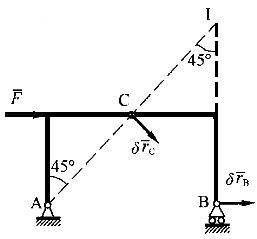 【點評】本題主要考察對于彈簧作功概念的掌握。 |
|
|
5.在正方體的一個側面沿AB方向作用一集中力 ,則該力對坐標軸的力矩大小為( )。 ,則該力對坐標軸的力矩大小為( )。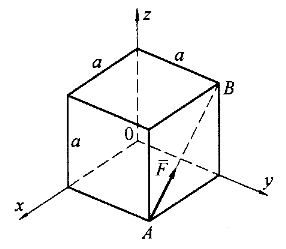 |
正確答案:D 解題思路:【解析】根據力對軸之矩的定義,M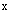 ( ( )=M )=M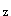 ( ( )= )= Fa,M Fa,M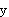 ( ( )=- )=-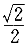 Fa。 Fa。【點評】本題主要考察力對軸之矩的概念及規定力矩正負的右手螺旋法則。 |
|
|
| 二、單選題 |
| (6-7題共用題干) |
均質桿AB的重量為4kg,置于光滑水平面上。在桿的B端作用一水平推力 =60N,使桿AB沿 =60N,使桿AB沿 的方向作直線平移。 的方向作直線平移。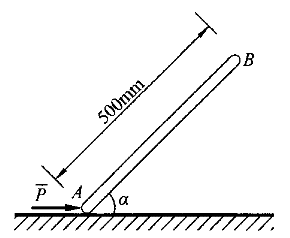 |
| 6.桿AB的加速度為( )。 |
| 7.桿AB的傾角α為( )。 |
| 正確答案:6.B;7.A 解題思路:1.【解析】考慮慣性力后對桿件列水平方向力的平衡方程。 【點評】本題主要考察慣性力的概念,以及達蘭貝爾原理的應用。 2.【解析】考慮慣性力后對桿件A點列力矩的平衡方程。 【點評】本題主要考察慣性力的概念,以及達蘭貝爾原理的應用。 |

