2012年一級注冊結構工程師考試普通物理考前沖刺(三)
發布時間:2012-07-25 共1頁
考前沖刺(三)
| 一、單選題 |
1.在一密閉容器中,儲有A、B、C三種處于平衡狀態的理想氣體,A種氣體的分子數密度為n.gif) ,它產生的壓強為p ,它產生的壓強為p.gif) ,B種氣體的分子數密度為2n ,B種氣體的分子數密度為2n.gif) ,C種氣體的分子數密度為3n ,C種氣體的分子數密度為3n.gif) ,則混合氣體的壓強p為( )。 ,則混合氣體的壓強p為( )。 |
正確答案:A 解題思路:【解析】設理想氣體的分子數密度為,n、壓強為P、溫度為T,則理想氣體狀態方程可以寫作P=nkT,式中k為玻耳茲曼常量。對于本題,A種氣體的分子數密度為n.gif) ,它產生的壓強為P ,它產生的壓強為P.gif) =n =n.gif) kT;B種氣體的分子數密度為2n kT;B種氣體的分子數密度為2n.gif) ,它產生的壓強為P ,它產生的壓強為P.gif) =2n =2n.gif) kT;C種氣體的分子數密度為3n kT;C種氣體的分子數密度為3n.gif) ,它產生的壓強為P ,它產生的壓強為P.gif) =3n =3n.gif) kT;則混合氣體的壓強P為P=P kT;則混合氣體的壓強P為P=P.gif) +P +P.gif) +p +p.gif) =6p =6p.gif) ;故選擇答案A。 ;故選擇答案A。【點評】本題是為了考察理想氣體狀態的另一種書寫形式P=nkT,該公式推導如下:設體積V的理想氣體中有N個分子,每個分子的質量為m .gif/f.gif) ,則N個分子的質量為:m-N·m ,則N個分子的質量為:m-N·m.gif/f.gif) ,1摩爾的理想氣體的質量為M=NA·m ,1摩爾的理想氣體的質量為M=NA·m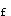 ,其中N ,其中N.gif/A_.gif) =6.022×10 =6.022×10.gif/~23.gif) mol mol.gif/~-1.gif) ,表示mol的氣體所含的分子數,稱為阿伏加德羅數。由理想氣體狀態方程:PV=(m/M)RT ,表示mol的氣體所含的分子數,稱為阿伏加德羅數。由理想氣體狀態方程:PV=(m/M)RT得: 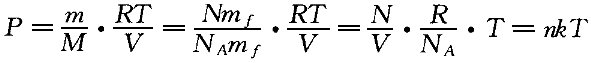 式中N/V是單位體積內的分子數;稱為分子數密度,k=R/N .gif/A_.gif) 是一個常量,稱為玻耳茲曼常量,其值為: 是一個常量,稱為玻耳茲曼常量,其值為:k=R/N 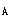 =8.31/6.022×10 =8.31/6.022×10 =1.38×10 =1.38×10 J·K J·K 因此,理想氣體狀態方程可以寫作P=nkT。理想氣體狀態有多種書寫形式,不同的書寫形式可揭示在不同的狀態下各量之間的關系,解題時要靈活應用。對于本題,可由P=nkT知,在一定的溫度下:P∝n,由此便可迅速解題。 因此,理想氣體狀態方程可以寫作P=nkT。理想氣體狀態有多種書寫形式,不同的書寫形式可揭示在不同的狀態下各量之間的關系,解題時要靈活應用。對于本題,可由P=nkT知,在一定的溫度下:P∝n,由此便可迅速解題。 |
|
|
| 2.駐波中,有下列關系式,其中不正確的是( )。 |
正確答案:D 解題思路:【解析】設沿正、負方向傳播的兩列波分別為: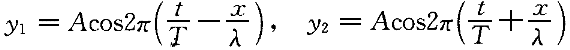 其合成波為: 其合成波為: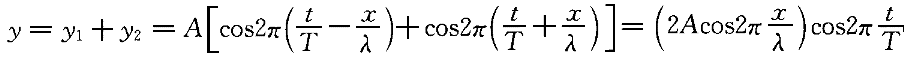 ;這就是駐波方程。由此式看出,合成以后的各點都在作同周期簡諧振動。當振幅最大值處,即波腹處, ;這就是駐波方程。由此式看出,合成以后的各點都在作同周期簡諧振動。當振幅最大值處,即波腹處,.gif/JZ104_322_30_2.gif) =1,得到波腹位置是:x=±k(λ/2)(k=0,1,2…);當振幅最小值處,即波節 =1,得到波腹位置是:x=±k(λ/2)(k=0,1,2…);當振幅最小值處,即波節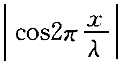 =0,得到波節位置是:x=±(2k+1)λ/4(k=0,1,2…) =0,得到波節位置是:x=±(2k+1)λ/4(k=0,1,2…)顯然,兩相鄰波節或波腹相距為λ/2。可見,A、B、C選項正確均正確,只有D選項錯誤。 【點評】本題考查了駐波的幾個結論。這幾個結論可以由駐波方程得到波腹位置公式: x=±k(λ/2)(k=0,1,2…) 波節位置公式: x=±(2k+1)λ/4(k=0,1,2…) 兩相鄰波節或波腹之間的距離為魯。 |
|
|
3.一個絕熱容器,用質量可忽略的絕熱板分成體積相等的兩部分。兩邊分別裝入質量相等、溫度相同的H.gif) 和O 和O.gif) 。開始時絕熱板P固定。然后釋放之,板P將發生移動(絕熱板與容器壁之間不漏氣且摩擦可以忽略不計)。在達到新的平衡位置后,若比較兩邊溫度的高低,則結果是( )。 。開始時絕熱板P固定。然后釋放之,板P將發生移動(絕熱板與容器壁之間不漏氣且摩擦可以忽略不計)。在達到新的平衡位置后,若比較兩邊溫度的高低,則結果是( )。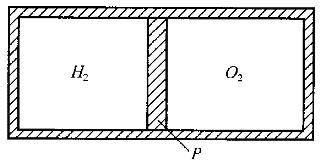 |
正確答案:B 解題思路:【解析】設初始狀態溫度為T.gif/0.gif) ,體積為V ,體積為V.gif) 。 。由理想氣體狀態方程:PV=(m/M)RT= .gif/ν.gif) RT得: RT得: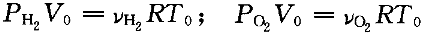 H .gif) 和O 和O.gif) 的摩爾數分別為: 的摩爾數分別為: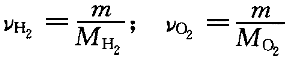 因為,兩氣體的質量相等、溫度相同,H 因為,兩氣體的質量相等、溫度相同,H.gif) 摩爾質量比O 摩爾質量比O.gif) 的摩爾質量小,所以, 的摩爾質量小,所以,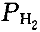 > >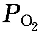 ,絕熱板P向右移動,直至達到新的平衡,此過程為絕熱過程。對H ,絕熱板P向右移動,直至達到新的平衡,此過程為絕熱過程。對H.gif) ,由絕熱過程方程有: ,由絕熱過程方程有: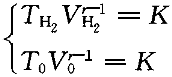 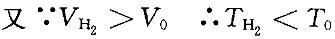 對O 對O.gif) ,由絕熱過程方程有: ,由絕熱過程方程有: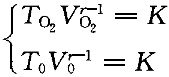  故,O 故,O.gif) 比H 比H.gif) 溫度高,故選B。 溫度高,故選B。【點評】此題考察的知識點較多。由理想氣體狀態方程PV=(m/M)RT= 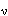 RT判斷壓強的大小,從而得出了板的移動方向是問題的關鍵,然后由絕熱過程方程分別判斷絕熱膨脹(Hz)和絕熱壓縮(02)對溫度的影響。 RT判斷壓強的大小,從而得出了板的移動方向是問題的關鍵,然后由絕熱過程方程分別判斷絕熱膨脹(Hz)和絕熱壓縮(02)對溫度的影響。 |
|
|
| 4.真空中波長為λ的單色光,在折射率為n的透明介質中,從A點沿某一路徑傳播到B點,已知A、B兩點的相位差為3π,則此路徑AB的光程為( )。 |
正確答案:B 解題思路:【解析】設A、B兩點的方向為z軸方向,A的坐標為x.gif) ,B的坐標為x ,B的坐標為x.gif) 。相位差與光程差的關系為:△φ=2π(δ/λ);設△x為AB兩點的距離,則A、B兩點的光程δ=n·△x 。相位差與光程差的關系為:△φ=2π(δ/λ);設△x為AB兩點的距離,則A、B兩點的光程δ=n·△x代入上式得:△φ=2πn△x/λ=3π;A、B兩點的光程為:n△x=(3/2)λ=1.5λ。 【點評】本題考查根據相位差與光程差的關系:△φ=2π(δ/λ)。已知光程差,可根據此公式求相位差,也可以用相位差來求光程差。 |
|
|
5.雙縫間距為0.5mm,被一波長為600nm(1nm=10.gif/~-9.gif) m)的單色光垂直照射,在縫后120cm處的屏上測得干涉條紋間距為( )。 m)的單色光垂直照射,在縫后120cm處的屏上測得干涉條紋間距為( )。 |
正確答案:D 解題思路:【解析】由楊氏雙縫干涉條紋間距公式得:△x=Dλ/d=1200/0.5×600×10 =1.44×10 =1.44×10 m=1.44mm m=1.44mm【點評】本題考查楊氏雙縫干涉條紋間距公式:△x=(D/d)λ;上式中d為雙縫間距,λ為入射波的波長,D為屏幕到雙縫之間的距離。2002年有類似考題。 |
|
|

