2012年一級注冊結構工程師考試普通物理考前沖刺(六)
發布時間:2012-07-25 共1頁
考前沖刺(六)
| 一、單選題 |
| 1.用波長為500nm的入射光照射在厚度均勻的透明塑料薄膜上,在反射角60°的位置上看到第10級干涉明條紋,薄膜折射率n=1.33,則薄膜的厚度是( )。 |
正確答案:B 解題思路:【解析】薄膜干涉的光程差為: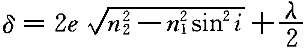 n  為膜的折射率,n 為膜的折射率,n 為空氣折射率,取n 為空氣折射率,取n =1 =1對明條紋 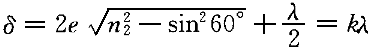 當i=60°時,看到第10級明條紋,取k=10,則: 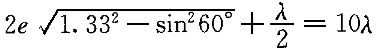 解得 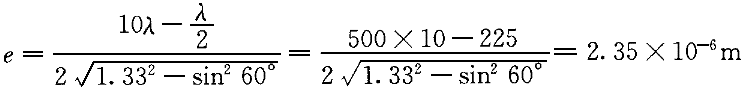 【點評】本題考查薄膜干涉的光程差公式及其相關運算。光程差為δ=2e× 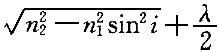 ,上表面反射光在反射時有半波損失,而下表面反射光在反射時無半波損失,所以有附加光程差λ/2。 ,上表面反射光在反射時有半波損失,而下表面反射光在反射時無半波損失,所以有附加光程差λ/2。 |
|
|
2.一定量的剛性雙原子分子氣體,開始時處于壓強為P =1.0×10 =1.0×10 Pa,體積為V Pa,體積為V =4×10 =4×10 m m.gif) ,溫度為T ,溫度為T =300K的狀態,后經等壓膨脹過程溫度上升到T =300K的狀態,后經等壓膨脹過程溫度上升到T =450K,再經絕熱過程溫度降回到T =450K,再經絕熱過程溫度降回到T =300K,求出整個過程中氣體對外做的功( )。 =300K,求出整個過程中氣體對外做的功( )。 |
正確答案:C 解題思路:【解析】由等壓過程方程V /T /T =V =V /T /T 得,等壓膨脹過程后,氣體的體積為:V 得,等壓膨脹過程后,氣體的體積為:V =(V =(V /T /T )T )T ;所以,等壓過程中氣體對外做的功 ;所以,等壓過程中氣體對外做的功W  =P =P (V (V -V -V )=200J;又將m/M=P )=200J;又將m/M=P V V /RT /RT 和C 和C =(5/2)R,代入絕熱過程做功公式,得絕熱過程做的功為: =(5/2)R,代入絕熱過程做功公式,得絕熱過程做的功為: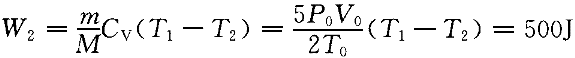 所以,整個過程做功為 所以,整個過程做功為W=W  +W +W =700J =700J【點評】在等壓過程中,狀態方程為V  /T /T =V =V /T /T ,功的公式為, ,功的公式為,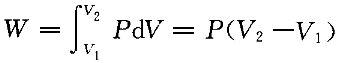 。在絕熱過程中,狀態方程為 。在絕熱過程中,狀態方程為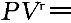 常數, 常數,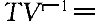 常數, 常數,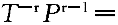 常數,功的公式:W=m/M·(i/2)R·(T 常數,功的公式:W=m/M·(i/2)R·(T -T -T ),或W=P ),或W=P V V -P -P V V /r-1。只有分清在什么過程中運用哪個公式,才可以正確解答本題。 /r-1。只有分清在什么過程中運用哪個公式,才可以正確解答本題。 |
|
|
| 3.兩瓶不同類型的理想氣體,設分子平均動能相等,但其分子數密度不相等,則( )。 |
正確答案:B 解題思路:【解析】由理想氣體壓強公式P=(2/3)n 可知,理想氣體壓強與分子數密度n和分子平均平動動能 可知,理想氣體壓強與分子數密度n和分子平均平動動能 有關,而理想氣體的溫度T=2 有關,而理想氣體的溫度T=2 /3k(或寫作 /3k(或寫作 =(3/2)jT)只與分子平均平動動能 =(3/2)jT)只與分子平均平動動能 有關。所以,兩瓶不同類型的理想氣體,分子平均動能相等,但其分子數密度不相等,則溫度相等但壓強不相等。故選擇答案B。 有關。所以,兩瓶不同類型的理想氣體,分子平均動能相等,但其分子數密度不相等,則溫度相等但壓強不相等。故選擇答案B。【點評】本題主要考察壓強和溫度分別與分子數密度n與分子平均平動動能  的關系。由理想氣體的溫度公式T=2 的關系。由理想氣體的溫度公式T=2 /3k可知,溫度與分子的平均平動動能成正比。由該公式可看出宏觀量溫度T與 /3k可知,溫度與分子的平均平動動能成正比。由該公式可看出宏觀量溫度T與 的關系,換句話說,該公式揭示了氣體溫度是統計意義,即氣體溫度是氣體分子平均平動動能的量度。并由此可知溫度是大量氣體分子熱運動的集體表現,具有統計意義,對個別分子,說它有溫度是沒有意義的。由理想氣體壓強公式P=(2/3)n 的關系,換句話說,該公式揭示了氣體溫度是統計意義,即氣體溫度是氣體分子平均平動動能的量度。并由此可知溫度是大量氣體分子熱運動的集體表現,具有統計意義,對個別分子,說它有溫度是沒有意義的。由理想氣體壓強公式P=(2/3)n 可知,壓強既和單位體積內的分子數成正比,又和分子的平均平動動能成正比。由于分子對器壁的碰撞是斷斷續續的,分子給與器壁的沖量是有起伏的,所以壓強是個統計平均量。在氣體中,分子數密度n也有起伏,所以n也是個統計平均值,理想氣體壓強公式表示三個統計平均量p、n和 可知,壓強既和單位體積內的分子數成正比,又和分子的平均平動動能成正比。由于分子對器壁的碰撞是斷斷續續的,分子給與器壁的沖量是有起伏的,所以壓強是個統計平均量。在氣體中,分子數密度n也有起伏,所以n也是個統計平均值,理想氣體壓強公式表示三個統計平均量p、n和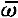 之間的關系,它是統計規律。 之間的關系,它是統計規律。 |
|
|
4.自然光從空氣入射到某介質表面上,當折射角為r =30°時,反射光是完全偏振光,則此介質的折射率為( )。 =30°時,反射光是完全偏振光,則此介質的折射率為( )。 |
正確答案:D 解題思路:【解析】由布儒斯特定律,反射光是完全偏振光時,i +r +r =90°,當折射角r =90°,當折射角r =30°時,入射角為i =30°時,入射角為i =60°因為,tani =60°因為,tani =n =n /n /n 并取空氣的折射率n 并取空氣的折射率n =1.0,經計算,介質的折射率為:n =1.0,經計算,介質的折射率為:n = =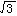 【點評】本題考察布儒斯特定律,有兩個知識點,第一,當入射角和折射角之和等于90°,即i  +r +r =90°時,反射光為線偏振光,稱此時的入射角i =90°時,反射光為線偏振光,稱此時的入射角i 為布儒斯特角。當i=i 為布儒斯特角。當i=i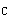 時,反射光線與折射光線垂直。第二,由折射定律:n 時,反射光線與折射光線垂直。第二,由折射定律:n sini sini =n =n sirnr sirnr =n =n cosi cosi 得:tani 得:tani =n =n.gif) /n /n.gif) ,i ,i 為自然光從第一種介質入射到第二種介質表面上的入射角,zz為第二種介質的折射率,咒,為第一種介質的折射率。 為自然光從第一種介質入射到第二種介質表面上的入射角,zz為第二種介質的折射率,咒,為第一種介質的折射率。 |
|
|
5.一平面簡諧波在t=0時的波形曲線如圖所示,波速u=0.08m/s,則該波的波動表達式為( )。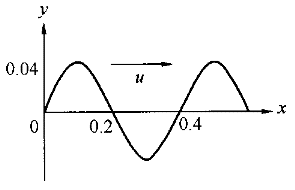 |
正確答案:B 解題思路:【解析】由圖可知,λ=0.4m,A=0.04m;波的頻率為:ν=u/λ=0.2Hz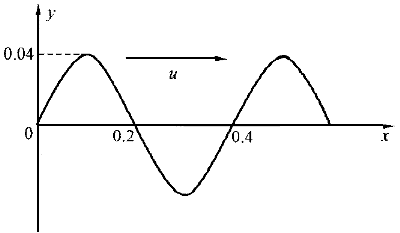 ; ;在t=0時刻O處質點向下運動,即y=0,初速度υ .gif) <0,由此可知0處,初相位φ=π2。所以O點處振動方程為: <0,由此可知0處,初相位φ=π2。所以O點處振動方程為:y=Acos(2πυt+π/2)波動表達式為: y=0.04cos[2π(0.2t-x/0.4)+π/2]即 y=0.04cos(0.4πt-5πx+π/2) 【點評】此題考查的內容較全面。首先,根據波形圖和已知條件求出波長、振幅、頻率和原點0點處振動方程,再由原點0點處振動方程和波的傳播方向求出波動方程。若坐標原點的振動方程為y=Acos(ωt+φ),則沿z軸正方向傳播的波的波動方程為:y=4cos[ω(t-x/u)+φ]。 |

